Density Of Air G Cm3 At Stp

For a better understanding of how temperature and pressure influence air density, let's focus on a case of dry air. It contains mostly molecules of nitrogen and oxygen that are moving around at incredible speeds. Use our particles velocity calculator to see how fast they can move! For example, the average speed of a nitrogen molecule with a mass of 14 u (u - unified atomic mass unit) at room temperature is about 670 m/s - two times faster than the speed of sound!

Moreover, at higher temperatures, gas molecules further accelerate. As a result, they push harder against their surroundings, expanding the volume of the gas . And the higher the volume with the same amount of particles, the lower the density. Therefore, air's density decreases as the air is heated. Note that every molecule listed is heavier that or equal to 18 u.

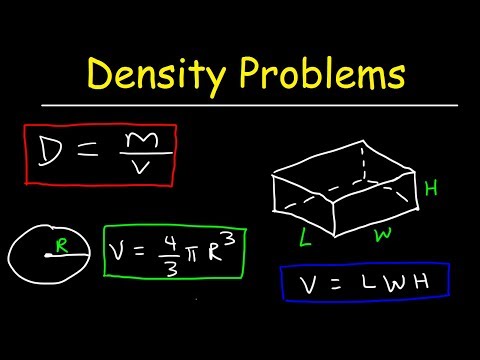
Now, let's add some water vapor molecules to the gas with the total atomic weight of 18 u (H₂O - two atoms of hydrogen 1 u and one oxygen 16 u). According to Avogadro's law, the total number of molecules remains the same in the container under the same conditions . It means that water vapor molecules have to replace nitrogen, oxygen or argon. Because molecules of H₂O are lighter than the other gases, the total mass of the gas decreases, decreasing the density of the air too. The density of air is usually denoted by the Greek letter ρ, and it measures the mass of air per unit volume (e.g. g / m3).

Dry air mostly consists of nitrogen (~78 %) and oxygen (~21 %). The remaining 1 % contains many different gases, among others, argon, carbon dioxide, neon or helium. However, the air will cease to be dry air when water vapor appears.

The earth's atmosphere exerts a pressure, as does any other gas. Although we do not normally notice atmospheric pressure, we are sensitive to pressure changes—for example, when your ears "pop" during take-off and landing while flying, or when you dive underwater. Gas pressure is caused by the force exerted by gas molecules colliding with the surfaces of objects .

Although the force of each collision is very small, any surface of appreciable area experiences a large number of collisions in a short time, which can result in a high pressure. In fact, normal air pressure is strong enough to crush a metal container when not balanced by equal pressure from inside the container. An online air density calculator such as the one by Engineering Toolbox let you calculate theoretical values for air density at given temperatures and pressures. The website also provides an air density table of values at different temperatures and pressures. These graphs show how density and specific weight decrease at higher values of temperature and pressure.

The density of air depends on many factors and can vary in different places. It mainly changes with temperature, relative humidity, pressure and hence with altitude . The air pressure can be related to the weight of the air over a given location. It is easy to imagine that the higher you stand, the less air is above you and the pressure is lower (check out our definition of pressure!). Therefore, air pressure decreases with increasing altitude.

In the following text, you will find out what is the air density at sea level and the standard air density. A common use of Equation 10.23 is to determine the molar mass of an unknown gas by measuring its density at a known temperature and pressure. This method is particularly useful in identifying a gas that has been produced in a reaction, and it is not difficult to carry out. A flask or glass bulb of known volume is carefully dried, evacuated, sealed, and weighed empty. It is then filled with a sample of a gas at a known temperature and pressure and reweighed.

The difference in mass between the two readings is the mass of the gas. The volume of the flask is usually determined by weighing the flask when empty and when filled with a liquid of known density such as water. The use of density measurements to calculate molar masses is illustrated in Example 10.

Use this air density calculator to instantly find how tightly packed an object's molecules are, allowing you to estimate the ρ parameter basing on the local temperature and pressure conditions. This value is vital for many further calculations, such as determining the aerodynamic drag forces or the performance of wind turbines. Continue reading to get a better understanding of the relationship between the local weather and ρ, and learn what air density levels you can expect in various regions. The calculator below can be used to calculate the air density and specific weight at given temperatures and atmospheric pressure. For any ideal gas, at a given temperature and pressure, the number of molecules is constant for a particular volume (see Avogadro's Law). So when water molecules are added to a given volume of air, the dry air molecules must decrease by the same number, to keep the pressure or temperature from increasing.

Hence the mass per unit volume of the gas decreases. Is defined as a hypothetical gaseous substance whose behavior is independent of attractive and repulsive forces and can be completely described by the ideal gas law. In reality, there is no such thing as an ideal gas, but an ideal gas is a useful conceptual model that allows us to understand how gases respond to changing conditions. As we shall see, under many conditions, most real gases exhibit behavior that closely approximates that of an ideal gas. The ideal gas law can therefore be used to predict the behavior of real gases under most conditions.

As you will learn in Section 10.8 "The Behavior of Real Gases", the ideal gas law does not work well at very low temperatures or very high pressures, where deviations from ideal behavior are most commonly observed. Standard temperature and pressure are a useful set of benchmark conditions to compare other properties of gases. The ideal gas law can be used to determine densities of gases. If the air isn't completely dry, you can also add some water molecules (​H2O​) which are two atomic units for the two hydrogen atoms and 16 atomic units for the singular oxygen atom. If you calculate how much mass of air you have, you can assume that these chemical constituents are distributed throughout it uniformly and then calculate the percent of these chemical components in dry air. To get a better idea of the density of air specifically, you need to account for how air is made of different gases when formulating its density.

At a constant temperature, pressure and volume, dry air is typically made of 78% nitrogen (​N2​), 21% oxygen (​O2​) and one percent argon (​Ar​). The ideal gas law allows us to calculate the value of the fourth variable for a gaseous sample if we know the values of any three of the four variables . Some applications are illustrated in the following examples. The approach used throughout is always to start with the same equation—the ideal gas law—and then determine which quantities are given and which need to be calculated. Let's begin with simple cases in which we are given three of the four parameters needed for a complete physical description of a gaseous sample. Dry air (0% humidity) is approximately 78% N2, 21% O2, and 1% Ar by moles.

Calculate the molar mass and density of dry air at 0 °C and 1.0 atm. Assume ideal behavior and use two significant figures in your answers. At constant pressure and volume, the density of a gas _____ as the molar mass increases. A gas made of larger particles will have a _____ density than a gas composed of smaller particles under the same conditions of temperature and pressure.

Atmospheric pressure is caused by the weight of the column of air molecules in the atmosphere above an object, such as the tanker car. At sea level, this pressure is roughly the same as that exerted by a full-grown African elephant standing on a doormat, or a typical bowling ball resting on your thumbnail. These may seem like huge amounts, and they are, but life on earth has evolved under such atmospheric pressure. If you actually perch a bowling ball on your thumbnail, the pressure experienced is twice the usual pressure, and the sensation is unpleasant. As you know, density is defined as the mass per unit volume of a substance. Since gases all occupy the same volume on a per mole basis, the density of a particular gas is dependent on its molar mass.

A gas with a small molar mass will have a lower density than a gas with a large molar mass. Gas density can be calculated from molar mass and molar volume. 15.Which one of the following statements is not consistent with the kinetic-molecular theory of gases?

The actual volume of the gas molecules themselves is very small compared to the volume occupied by the gas at ordinary temperatures and pressures. The average kinetic energies of different gases are different at the same temperature. There is no net gain or loss of the total kinetic energy in collisions between gas molecules. The theory explains most of the observed behavior of gases at ordinary temperatures and pressures. Calculate the number of molecules in a cubic meter of gas at standard temperature and pressure , which is defined to be 0ºC and atmospheric pressure.

At room temperatures, collisions between atoms and molecules can be ignored. In this case, the gas is called an ideal gas, in which case the relationship between the pressure, volume, and temperature is given by the equation of state called the ideal gas law. In which ​ρ​ is density in units of ​m/V​ mass/volume (kg/m3). Keep in mind this version of the ideal gas law uses the ​R​ gas constant in units of mass, not moles. Air - Specific Heat vs. Temperature at Constant Pressure - Online calculator with figures and tables showing specific heat of dry air vs. temperature and pressure.

The reaction of a copper penny with nitric acid results in the formation of a red-brown gaseous compound containing nitrogen and oxygen. A sample of the gas at a pressure of 727 mmHg and a temperature of 18°C weighs 0.289 g in a flask with a volume of 157.0 mL. Calculate the molar mass of the gas and suggest a reasonable chemical formula for the compound.

The density of gases have been listed below in alphabetical order in the units of both metric and imperial. The chemical formula as well as molar mass has also been listed. The properties of N2 will deviate more from ideality at -100oC than at 100oC. Van der Waal's equation corrects for the non-ideality of real gases.

Molecules of CH4 at high pressures and low temperatures have no attractive forces between each other. Molecules of an ideal gas are assumed to have no significant volume. Ρ is the object's density m is the object's total mass V is the object's total volume Under specified conditions of temperature and pressure, the density of a fluid is defined as described above.

However, the density of a solid material can be defined in several ways. Porous or granular materials have a density of the solid material, as well as a bulk density, which can be variable. For example, if you gently fill a container with sand, and divide the mass of sand by the container volume you get a value termed loose bulk density. If you took this same container and tapped on it repeatedly, allowing the sand to settle and pack together, and then calculate the results, you get a value termed tapped or packed bulk density.

Tapped bulk density is always greater than or equal to loose bulk density. In both types of bulk density, some of the volume is taken up by the spaces between the grains of sand. The density of the sand grains, exclusive of the air between the grains, will be higher than the bulk density.

The ideal gas law can be considered to be another manifestation of the law of conservation of energy . Work done on a gas results in an increase in its energy, increasing pressure and/or temperature, or decreasing volume. This increased energy can also be viewed as increased internal kinetic energy, given the gas's atoms and molecules. Use the ideal gas law to calculate pressure change, temperature change, volume change, or the number of molecules or moles in a given volume. Air pressure is a physical property of a gas that tells us with how much strength it has when acting on the surroundings. Let's consider a cubic container with some air closed inside.

According to the kinetic theory of gases, the molecules of the gas are in constant motion with a velocity that depends on the thermal energy. Particles collide with each other and with the walls of a container, exerting a tiny force on them. However, since the number of the enclosed molecules reaches about ~10²³ (order of magnitude of Avogadro's constant), the total force becomes significant and measurable - this is pressure. Argon - Density and Specific Weight - Online calculator, figures and tables showing density and specific weight of argon, Ar, at varying temperature and pressure - Imperial and SI Units. The ideal gas law relates the pressure and volume of a gas to the number of gas molecules and the temperature of the gas. Atoms and molecules are close together in solids and liquids.

Thus gases have lower densities than liquids and solids. Density is mass per unit volume, and volume is related to the size of a body cubed. So if the distance between atoms and molecules increases by a factor of 10, then the volume occupied increases by a factor of 1000, and the density decreases by a factor of 1000. The equilibrium vapor pressure of water is the pressure exerted by a vapor that is in thermodynamic equilibrium with its liquid phase at a given temperature.

It is a measure of the tendency of molecules or atoms to escape from a surface of a liquid and become a gas. As the temperature increases, the equilibrium vapor pressure increases too. Because of these dependencies and the fact that the Earth's atmosphere contains various gases the air density definition needs to be further expanded.

A proper modification has been made in our air density calculator with the density of air formula shown in the section called "How to calculate the air density?". To find the density of a gas, the volume and the mass must be known. At STP both of these quantities are known, as 1 mole of any gas occupies cm3. It is, therefore, a simple matter of dividing the molar mass by to obtain the density.

The values produced, however, are very small and gas densities are instead often quoted in grams per litre for this very reason. It is important to check your answer to be sure that it makes sense, just in case you have accidentally inverted a quantity or multiplied rather than divided. In this case, the temperature of the gas decreases. Because we know that gas volume decreases with decreasing temperature, the final volume must be less than the initial volume, so the answer makes sense. We could have calculated the new volume by plugging all the given numbers into the ideal gas law, but it is generally much easier and faster to focus on only the quantities that change.

Thus the ideal gas law does a good job of approximating the behavior of real gases at STP. We can use the ideal gas equation to calculate the volume of 1 mole of an ideal gas at 0°C and 1 atmosphere pressure. As all gases that are behaving ideally have the same number density, they will all have the same molar volume. This is useful if you want to envision the distance between molecules in different samples. For instance if you have a sample of liquid water, it has a mass density of 1 g mL–1.

Black Clubs Near Me Open Now

The Black Panther Party , originally the Black Panther Party for Self-Defense, was a Marxist-Leninist Black Power political organization founded by college students Bobby Seale and Huey P. Newton in October 1966 in Oakland, California. The party was active in the United States between 1966 and 1982, with chapters in many major cities and international chapters in Britain and Algeria. Upon its inception the Black Panther Party's core practice was its open carry armed citizens' patrols ("copwatching") to monitor the behavior of officers of the Oakland Police Department and challenge police brutality in the city. From 1969 onwards, a variety of community social programs became a core activity.

The Party instituted the Free Breakfast for Children Programs to address food injustice, and community health clinics for education and treatment of diseases including sickle cell anemia, tuberculosis, and later HIV/AIDS. It advocated for class struggle, with the party representing the proletarian vanguard. Black Panther Party membership reached a peak in 1970, with offices in 68 cities and thousands of members, but it began to decline over the following decade. After its leaders and members were vilified by the mainstream press, public support for the party waned, and the group became more isolated.[deprecated source?

] In-fighting among Party leadership, fomented largely by the FBI's COINTELPRO operation, led to expulsions and defections that decimated the membership. Popular support for the Party declined further after reports of the group's alleged criminal activities, such as drug dealing and extortion of Oakland merchants. By 1972 most Panther activity centered on the national headquarters and a school in Oakland, where the party continued to influence local politics. Though under constant police surveillance, the Chicago chapter also remained active and maintained their community programs until 1974.

The Seattle chapter persisted longer than most, with a breakfast program and medical clinics that continued even after the chapter disbanded in 1977. The Party continued to dwindle throughout the 1970s, and by 1980 had just 27 members. During World War II, tens of thousands of black people left the Southern states during the Second Great Migration, moving to Oakland and other cities in the Bay Area to find work in the war industries such as Kaiser Shipyards. The sweeping migration transformed the Bay Area as well as cities throughout the West and North, altering the once white-dominated demographics. A new generation of young black people growing up in these cities faced new forms of poverty and racism unfamiliar to their parents, and they sought to develop new forms of politics to address them. Black Panther Party membership "consisted of recent migrants whose families traveled north and west to escape the southern racial regime, only to be confronted with new forms of segregation and repression".

In the early 1960s, the Civil Rights Movement had dismantled the Jim Crow system of racial caste subordination in the South with tactics of non-violent civil disobedience, and demanding full citizenship rights for black people. However, not much changed in the cities of the North and West. Northern and Western police departments were almost all white.

In 1966, only 16 of Oakland's 661 police officers were African American (less than 2.5%). In early 1972, the party began closing down dozens of chapters and branches all over the country and bringing members and operations to Oakland. The political arm of the southern California chapter was shut down and its members moved to Oakland, although the underground military arm remained for a time. The underground remnants of the LA chapter, which had emerged from the Slausons street gang, eventually re-emerged as the Crips, a street gang who at first advocated social reform before devolving into racketeering.

Minister of Education Ray "Masai" Hewitt created the Buddha Samurai, the party's underground security cadre in Oakland. Newton expelled Hewitt from the party later in 1972, but the security cadre remained in operation under the leadership of Flores Forbes. One of the cadre's main functions was to extort and rob drug dealers and after-hours clubs.

In late October 1966, Huey P. Newton and Bobby Seale founded the Black Panther Party (originally the Black Panther Party for Self-Defense). In formulating a new politics, they drew on their work with a variety of Black Power organizations. Newton and Seale first met in 1962 when they were both students at Merritt College.

They joined Donald Warden's Afro-American Association, where they read widely, debated, and organized in an emergent black nationalist tradition inspired by Malcolm X and others. Eventually dissatisfied with Warden's accommodationism, they developed a revolutionary anti-imperialist perspective working with more active and militant groups like the Soul Students Advisory Council and the Revolutionary Action Movement. Police killed or incarcerated many male leaders, but female Panthers were less targeted for much of the 1960s and 1970s. By 1968, women made up two-thirds of the party, while many male members were out of duty.

In the absence of much of the original male leadership, women moved into all parts of the organization. Roles included leadership positions, implementing community programs, and uplifting the black community. Women in the group called attention to sexism within the Party, and worked to make changes from within. Significant disagreements among the Party's leaders over how to confront ideological differences led to a split within the party. Certain members felt that the Black Panthers should participate in local government and social services, while others encouraged constant conflict with the police. In January 1971, Newton expelled Geronimo Pratt who, since 1970, had been in jail facing a pending murder charge.

Newton also expelled two of the New York 21 and his own secretary, Connie Matthews, who flee the country. The Free Breakfast For Children program was especially significant because it served as a space for educating youth about the current condition of the Black community, and the actions that the Party was taking to address that condition. The breakfast program became so popular that the Panthers Party claimed to have fed twenty thousand children in the 1968–69 school year.

At the 1968 Summer Olympics, Tommie Smith and John Carlos, two American medalists, gave the black power salute during the American national anthem. The International Olympic Committee banned them from all future Olympic Games. Film star Jane Fonda publicly supported Huey Newton and the Black Panthers during the early 1970s.

She actually ended up informally adopting the daughter of two Black Panther members, Mary Luana Williams. Fonda and other Hollywood celebrities became involved in the Panthers' leftist programs. The "Free Huey" campaign attracted black power organizations, New Left groups, and other activist groups such as the Progressive Labor Party, Bob Avakian of the Community for New Politics, and the Red Guard. For example, the Black Panther Party collaborated with the Peace and Freedom Party, which sought to promote a strong antiwar and antiracist politics in opposition to the establishment democratic party. The Black Panther Party provided needed legitimacy to the Peace and Freedom Party's racial politics and in return received invaluable support for the "Free Huey" campaign.

In August 1967, the Federal Bureau of Investigation instructed its program "COINTELPRO" to "neutralize ... black nationalist hate groups" and other dissident groups. In September 1968, FBI Director J. Edgar Hoover described the Black Panthers as "the greatest threat to the internal security of the country". By 1969, the Black Panthers and their allies had become primary COINTELPRO targets, singled out in 233 of the 295 authorized "Black Nationalist" COINTELPRO actions. The goals of the program were to prevent the unification of militant black nationalist groups and to weaken their leadership, as well as to discredit them to reduce their support and growth. In October 1977 Flores Forbes, the party's assistant chief of staff, led a botched attempt to assassinate Crystal Gray, a key prosecution witness in Newton's upcoming trial, who had been present the day of Kathleen Smith's murder. When three Panthers attacked the wrong house by mistake, the occupant returned fire and killed one of the Panthers, Louis Johnson, while the other two assailants escaped.

One of them, Flores Forbes, fled to Las Vegas, Nevada, with the help of Panther paramedic Nelson Malloy. Fearing that Malloy would discover the truth behind the botched assassination attempt, Newton allegedly ordered a "house cleaning", and Malloy was shot and buried alive in the desert. Although permanently paralyzed from the waist down, Malloy escaped and told police that fellow Panthers Rollin Reid and Allen Lewis were behind his attempted murder.

Newton denied any involvement or knowledge and said the events "might have been the result of overzealous party members". Newton focused the BPP on the Party's Oakland school and various other social service programs. In early 1971, the BPP founded the "Intercommunal Youth Institute" in January 1971, with the intent of demonstrating how black youth ought to be educated. Ericka Huggins was the director of the school and Regina Davis was an administrator.

The school was unique in that it did not have grade levels but instead had different skill levels so an 11-year-old could be in second-level English and fifth-level science. Elaine Brown taught reading and writing to a group of 10- to 11-year-olds deemed "uneducable" by the system. The school children were given free busing; breakfast, lunch, and dinner; books and school supplies; children were taken to have medical checkups; many children were given free clothes. Former FBI agent Wesley Swearingen asserts that the Bureau was guilty of a "plot to murder" the Panthers. Hampton had been slipped the barbiturates which had left him unconscious by William O'Neal, who had been working as an FBI informant. Hanrahan, his assistant and eight Chicago police officers were indicted by a federal grand jury over the raid, but the charges were later dismissed.

In 1979 civil action, Hampton's family won $1.85 million from the city of Chicago in a wrongful death settlement. Hampton was sleeping next to his pregnant fiancée and was subsequently shot twice in the head at point-blank range while unconscious. Coroner reports show that Hampton was drugged with a powerful barbiturate that night, and would have been unable to have been awoken by the sounds of the police raid. Seven other Panthers sleeping at the house at the time of the raid were then beaten and seriously wounded, then arrested under charges of aggravated assault and attempted murder of the officers involved in the raid.

The BPP adopted a "Serve the People" program, which at first involved a free breakfast program for children. By the end of 1968, the BPP had established 38 chapters and branches, claiming more than five thousand members. Eldridge and Kathleen Cleaver left the country days before Cleaver was to turn himself in to serve the remainder of a thirteen-year sentence for a 1958 rape conviction.

Although at the time the BPP claimed that the police had ambushed them, several party members later admitted that Cleaver had led the Panther group on a deliberate ambush of the police officers, provoking the shoot-out. Seven other Panthers, including Chief of Staff David Hilliard, were also arrested. Hutton's death became a rallying issue for Panther supporters. Newsreel in which Kathleen Cleaver spoke at Hutton Memorial Park in Alameda County, California. The footage also shows a student protest demonstration at Alameda County Courthouse, Oakland, California. Black Panther Party members are shown as they marched in uniform.

Students at the rally marched, sang, clapped hands, and carried protest signs. After your meal, you can choose from a wide variety of entertainment options, including bars, clubs, cigar lounges, comedy shows, live music performances, and even rooftop escapes to avoid the crowded and busy streets. This is a one stop shop where everything is within a five minute walking distance and will surely make your night unforgettable. Come to the Gaslamp District today and experience the heart and soul of San Diego. We opened shop in 1982 and have been providing an excellent clubbing experience ever since.

Our sole mission is to provide you great music and a large space where you can show off your skills. People with different taste in music visit our club which why we play different music each night. On Wednesdays, we play local DJ's and Chicago based artist's music.

On Saturdays, Techno music is played, and Sundays are Disco nights. The Black Panther Party was involved in many community projects as part of their organization. These projects included community outreach, like the breakfast program, education, and health programs. In many cases women were the ones primarily involved with administering these types of programs.

In 1974, Huey Newton and eight other Panthers were arrested and charged with assault on police officers. In August 1974, Newton went into exile in Cuba to avoid prosecution for the murder of Kathleen Smith, an eighteen-year-old prostitute. Newton was also indicted for pistol-whipping his tailor, Preston Callins. Newton was also acquitted of assaulting Preston Callins after Callins refused to press charges. In late September 1971, Huey P. Newton led a delegation to China and stayed for 10 days.

During the trip, the Chinese arranged for him to meet and have dinner with a DPRK ambassador, a Tanzanian ambassador, and delegations from both North Vietnam and the Provisional Revolutionary Government of South Vietnam. Huey was under the impression he was going to meet Mao Zedong, but instead had two meetings with the first Premier of the People's Republic of China Zhou Enlai. One of these meetings also included Mao Zedong's wife Jiang Qing. Huey described China as "a free and liberated territory with a socialist government". Some Panther leaders, such as Huey P. Newton and David Hilliard, favored a focus on community service coupled with self-defense; others, such as Eldridge Cleaver, embraced a more confrontational strategy.

In February 1971, Eldridge Cleaver deepened the schism in the party when he publicly criticized the Party for adopting a "reformist" rather than "revolutionary" agenda and called for Hilliard's removal. Cleaver was expelled from the Central Committee but went on to lead a splinter group, the Black Liberation Army, which had previously existed as an underground paramilitary wing of the Party. The split turned violent, as the Newton and Cleaver factions carried out retaliatory assassinations of each other's members, resulting in the deaths of four people. From mid-to-late 1971, hundreds of members throughout the country quit the Black Panther Party. When Algeria held its first Pan-African Cultural Festival, they invited many important figures from the United States. Among the important figures invited to the festival were Bobby Seale and Eldridge Cleaver.

The cultural festival allowed Black Panthers to network with representatives of various international anti-imperialist movements. This was a significant time, which led to the formation of the International Section of the Party. It is at this festival that Cleaver met with the ambassador of North Korea, who later invited him to an International Conference of Revolutionary Journalists in Pyongyang. Eldridge also met with Yasser Arafat, and gave a speech supporting the Palestinians and their goal of achieving liberation.

In 1968, the group shortened its name to the Black Panther Party and sought to focus directly on political action. Members were encouraged to carry guns and to defend themselves against violence. An influx of college students joined the group, which had consisted chiefly of "brothers off the block". Some members were more interested in supporting the Panthers' social programs, while others wanted to maintain their "street mentality".

The initial tactic of the party utilized contemporary open-carry gun laws to protect Party members when policing the police. This act was done to record incidents of police brutality by distantly following police cars around neighborhoods. When confronted by a police officer, Party members cited laws proving they had done nothing wrong and threatened to take to court any officer that violated their constitutional rights. Between the end of 1966 to the start of 1967, the Black Panther Party for Self-Defense's armed police patrols in Oakland black communities attracted a small handful of members.

Numbers grew slightly starting in February 1967, when the party provided an armed escort at the San Francisco airport for Betty Shabazz, Malcolm X's widow and keynote speaker for a conference held in his honor. The party enrolled the most members and had the most influence in the Oakland-San Francisco Bay Area, New York, Chicago, Los Angeles, Seattle, and Philadelphia. There were active chapters in many prisons, at a time when an increasing number of young African-American men were being incarcerated. Huey Newton allegedly killed officer John Frey in 1967, and Eldridge Cleaver led an ambush in 1968 of Oakland police officers, in which two officers were wounded and Panther Bobby Hutton was killed. FBI infiltrators caused the party to suffer many internal conflicts, resulting in the murders of Alex Rackley and Betty Van Patter.