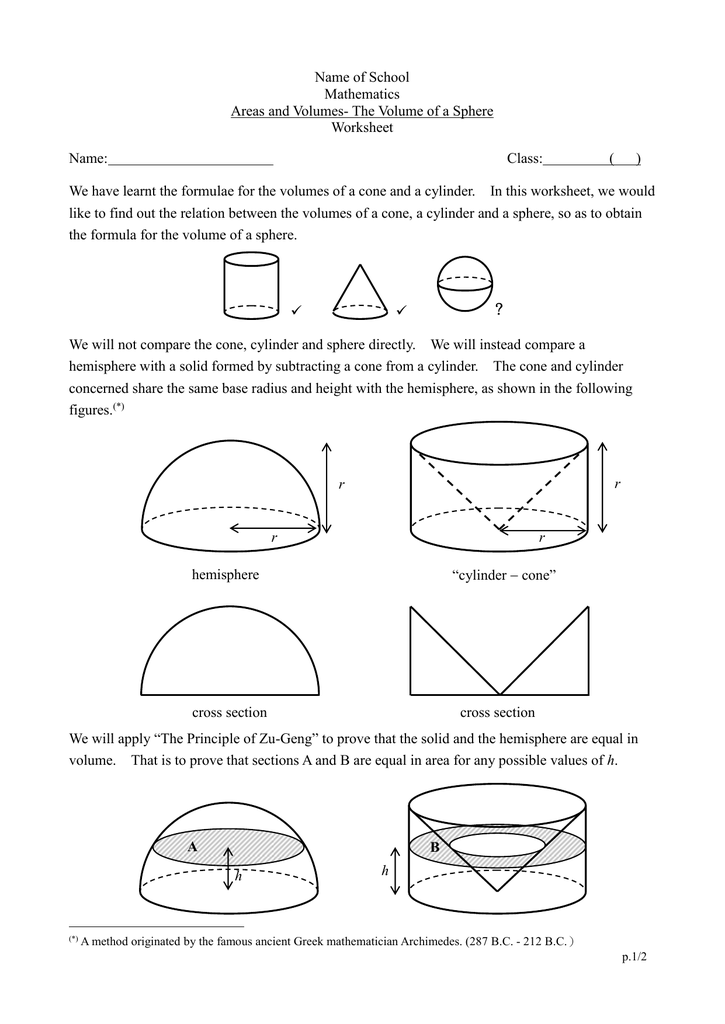
To find the volume of a sphere, we can calculate the volume by using a simple volume formula where we multiply 4/3 by pi by the radius cubed. The volume of sphere formula is unique because it only requires the radius to calculate the volume of any sphere. When finding the volume of spheres, it is important to note if we are given the radius or the diameter of the shape.
This formula is very similar to other prism volume formulas. Find the limits of integration on the triple integral for the volume of the sphere using Cartesian and spherical coordinates and the function to be integrated. In this blog, I derived the expression for the surface area of a sphere, .
In today's blog, I will derive the expression for the volume of a sphere. Actually, once one has understood how to derive the surface area of a sphere using spherical polar coordinates, deriving the volume is pretty straight forward. The unit of volume of a sphere is given as the 3. The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet.
The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere. There are two types of spheres, solid sphere, and hollow sphere. The volume of both types of spheres is different.
We will learn in the following sections about their volumes. Using this method, Archimedes was able to show that a cone had the same volume as a a pyramid with the same base area and height. Consider a sphere of radius r and divide it into pyramids. A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface.
The formulas for the volume and surface area of a sphere are given below. A simple check on any formula for area or volume is a dimensional check. Area is the two-dimensional amount of space that an object occupies.
Area is measured along the surface of an object and has dimensions of length squared; for example, square feet of material, or square centimeters. Volume is the three-dimensional amount of space that an object occupies. Volume has dimensions of length cubed; for example, cubic feet of material, or cubic centimeters (cc's). One can calculate theweightof any object by multiplying thedensityof the material by the volume of the object.
On this slide, we list some equations for computing the volume of objects which often occur in aerospace. There are similar equations for computing theareaof objects. The magnitude of theaerodynamic forcesdepends on the surface area of an object, while thegravitational forceand certainthermodynamic effectsdepend on the volume of the object.
The equations to compute area and volume are used every day by design engineers. Try deriving for yourself the volume of a sphere by integration. You can start with a surface of a sphere with zero radius, and integrate that out to the radius of your sphere. Think of that as having a a series of infinitesimally thin concentric shells from the center of the sphere out to the full radius of the sphere. That operation will "sweep" through all the volume of the sphere, accumulating the total volume of the sphere. So volume is equal to 288 pi and then we have to write in our units, cubic centimetres.
So there's only one dimension you need to know in order to calculate the volume of a sphere and that is your radius. In this problem we had to divide 12 in half because there was a diameter so we could substitute and find our volume. A spherical volume can be assumed to be constituted of a large number of thin circular disks of continuously varying radii kept over one another with their centres collinear. We have to choose one of these elementary disks.
A thin disk element of radius r and thickness dy located at a distance of y from the horizontal axis has been focused. Its volume can be written as the multiplication of base area πr² and thickness dy. Further, the disc radius r can be expressed in terms of vertical dimension y using the Pythagoras theorem.
We can use triple integrals and spherical coordinates to solve for the volume of a solid sphere. This statement is not at all obvious or elementary. "A sphere's volume is two cones of equal height and radius to that of the sphere's". The assertion about the cone and the cylinder is a little easier to prove, but it too is not obvious.
So you have not really provided an answer to this to year old question. I think the accepted answer is closest to what you have in mind. If you want to help here I think you should pay attention to new questions that don't yet have answers.
Now the question becomes calculating the volume of the bicylinder . It is also very difficult, so add a cube packing the bicylinder . Now when the plane intersects the cube, it forms another larger square. The extra area in the large square , is the same as 4 small squares . Moving through the whole bicylinder generates a total of 8 pyramids. The volume of a sphere is the three-dimensional space occupied by a sphere.
This volume depends on the radius of the sphere (i.e, the distance of any point on the surface of the sphere from its centre). If we take the cross-section of the sphere then the radius can be calculated by reducing the length of the diameter to its half. Or we can also say that the radius is half of the diameter.
A circle can be drawn on a paper but a sphere can't be drawn on a piece of paper. This is because Circle is a two-dimensional figure whereas a sphere is a three-dimensional object, example- Ball, Earth, etc. A Sphere is a 3D figure whose all the points lie in the space. All the points on the surface of a sphere are equidistant from its centre.
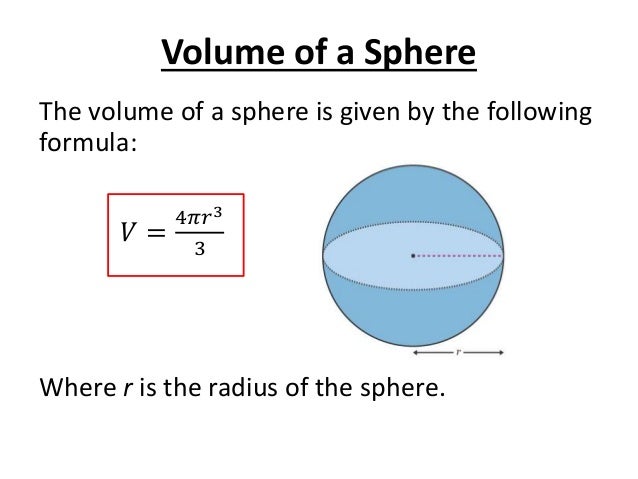
This distance from the surface to the centre is called the radius of the sphere. Use the formula derived in the previous problem to calculate the volume of a hemisphere with radius 2 inches. In the following problems, students will calculate the volume of a sphere using the formula derived in the lesson. Then, students will derive the formula for the volume of a hemisphere using a similar integration technique.
Last, students will use their new formula to find the volume of a specific hemisphere. In our daily life, we come across different types of spheres. Basketball, football, table tennis, etc. are some of the common sports that are played by people all over the world. The balls used in these sports are nothing but spheres of different radii.
The volume of sphere formula is useful in designing and calculating the capacity or volume of such spherical objects. You can easily find out the volume of a sphere if you know its radius. It is far from obvious from the figure above how the cone and sphere add up to the cylinder. However, if we `rearrange' the conic volume, things become clearer.
We note that a cone with half the height () has half the volume. So, we replace the cone by a double cone, each half of height , with centre-point at the centre of the sphere . Now it is clear that in a horizontal slice, the cross-section of the sphere is greatest at the equator and least at the poles. Contrariwise, the cross-section of the cone is greatest near the top and bottom, and least near the centre-point.
Thus, it is not unreasonable to speculate that the sum of the two cross-section areas might be equal. There is another special formula for finding the volume of a sphere. The volume is how much space takes up the inside of a sphere. The answer to a volume question is always in cubic units. Let the inside of a sphere of radius r be composed of n square pyramids, each with a height of r and a base with an area of A. The apex of each pyramid is at the center of the sphere, as shown below.
The following video shows how to solve problems involving the formulas for the surface area and volume of spheres. Also, take a hollow right-circular cylinder having the base radius r and height equal to 2r (see Figure 41.1). So let's look at a quick example about how we could use that formula. Here we have a sphere and we're being asked to find its volume. Now notice that what they give you is not a radius but a diameter.
So we're going to start off by writing our formula, volume equals four thirds pi times your radius cubed. Use spherical coordinates to find the volume of the triple integral, where ??? A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center.
The volume of a sphere is measured in cubic units. Also on that page you will see an explanation of the 4/3 in the volume of the sphere. In brief, you can imagine drawing a tiny triangle on the surface of the sphere and connecting its corners to the center of the sphere. The volume of a pyramid is 1/3 times the area of the base times the height.
Thus the volume of this pyramid is 1/3 times the radius of the sphere, times the area of that little triangle. This is the figure described in the question. The sphere is there for comparison; the cylinder has had a cone drilled out from the top and the bottom, leaving solid material around it.
We're going to slice both the cylinder and the sphere at a height h above the center. But for students who only know geometry, "wait until you learn calculus" can be unsatisfying. Fortunately, there are a couple ways to do it using only geometrical ideas . The important thing is that they can be followed without deep knowledge. In this lesson, we derive the formula for finding the volume of a sphere.
This formula is derived by integrating differential volume elements formed by slicing the sphere into cylinders with a differential thickness. Archimedes invented a method that was later re-discovered and became known as Cavalieri's principle. This involves slicing solids with a family of parallel planes. In particular, if we have two solids and if each plane cuts them both into cross-sections of equal area, then the two solids have equal volumes. One of the most remarkable and important mathematical results obtained by Archimedes was the determination of the volume of a sphere.
Archimedes used a technique of sub-dividing the volume into slices of known cross-sectional area and adding up, or integrating, the volumes of the slices. This was essentially an application of a technique that was — close to two thousand years later — formulated as integral calculus. In the figure below, only one of such pyramid is shown. Now something that you should notice is that we have r to the third which reminds you that we are talking about volume and not a surface area.
So we said that r is going to be half of 12, since 12 is our diameter. So volume equals four thirds times pi times 6 cubed. So we say volume is equal to four thirds pi times 216. I'm going to multiply four thirds by 216 on my calculator. I should end up with some number larger than 216 and I do.
Okay, so suppose we have hemisphere of radius . Suppose also that we have a cylinder of height and radius . Finally suppose we cut a cone of height and radius from the cylinder and call the resulting shape .. Usually these volume and area formulas are derived using calculus; but they were first worked out by the Greeks, notably Archimedes, using geometrical methods. The complete proof of the formulas can be a little involved, but I can give you the basic idea. I like to start with the area of the sphere, and get the volume from that - that covers two questions at once.


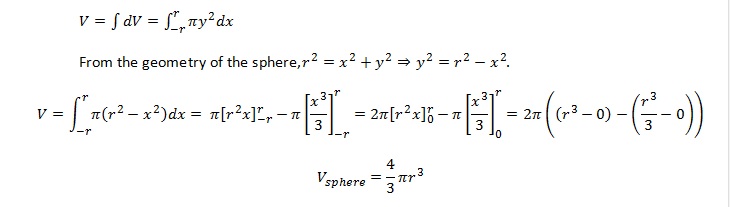














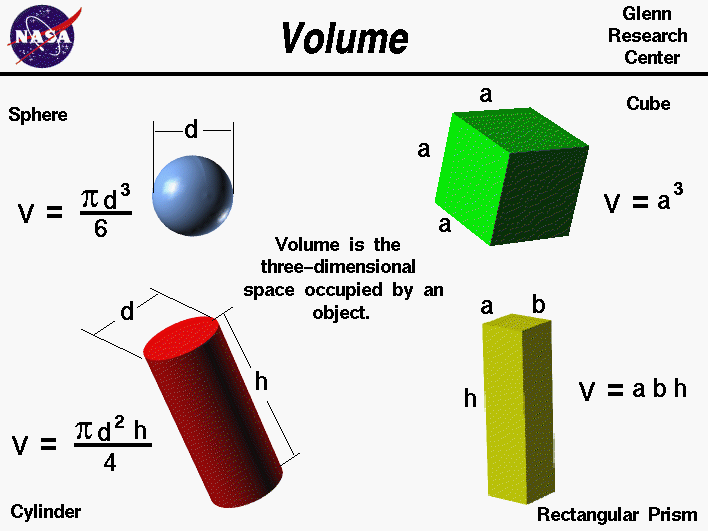




No comments:
Post a Comment
Note: Only a member of this blog may post a comment.